
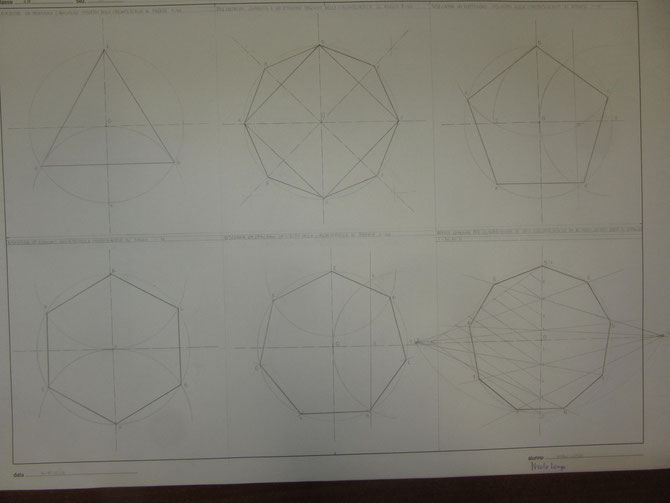
TAV.5-POLIGONI REGOLARI INSCRITTI NELLA CIRCONFERENZA
1)Disegnare un triangolo equilatero inscritto nella circonferenza di raggio r=50.
2)Disegnare un quadrato e un ottagono inscritti nella circonferenza di raggio r=50.
3)Disegnare un pentagono regolare inscritto nella circonferenza di raggio r=50.
4)Disegnare un esagono regolare inscritto nella circonferenza di raggio r=50.
5)Disegnare un ettagono regolare inscritto nella circonferenza di raggio r=50.
6)Regola generale per la suddivisione di una circonferenza in n parti uguali dato il raggio r=50. Es.n=9.
Es.1 Tav.5- Disegnare un triangolo equilatero inscritto nella circonferenza di raggio r=50. (Suddividere una circonferenza in tre parti uguali)
1) Tracciare una circonferenza di centro O e di raggio r=50.
2) Tracciare gli assi principali che individuano i punti 1 e C sulla circonferenza.
3) Puntare il compasso in 1 con raggio 1-O e descrivere un arco che taglia la circonferenza nei punti A e B.
4) Unire C ad A e B con linea continua evidente; ABC è il triangolo equilatero inscritto.
Es.n2 Tav5- Disegnare un quadrato e un ottagono regolare inscritti nella circonferenza di raggio 50
1)Disegnare la circonferenza di centro O e raggio 50.
2)Disegnare i 2 assi principali che si intersecano perpendicolarmente al centro.
3)Si individuano così sulla circonferenza i punti A, B, C, D e uniendoli si ottiene un quadrato ruotato di 45°
4)Costruire la bisettrice dell’angolo AOD e dell’angolo DOE;trovo sulla circonf. i punti H, E, F e G.
5)Unendo tutti i punti così trovati si ottiene un ottagono.
(Giraldi Nicolò)
Es.n3 Tav5- Disegnare un pentagono regolare inscritto nella circonferenza di raggio r=50
- Tracciare la circonf. di raggio r=50.
- Costruire i due assi principali, tra loro ortogonali, che individuano i punti D e 1 sulla circonferenza.
- Costruire l'asse del segmento O-1 individuando il punto M.
- Si centra in M con apertura di compasso M-D e si traccia un arco di circonferenza che interseca il raggio opposto a O1 nel punto 2.
- D2 individua la dimensione del lato del pentagono.
- Si centra in D con apertura di compasso D-2 e si individua il punto E sulla circonf.
- Riportando la misura di DE sulla circonferenza, si trovano i punti A,B,C.
- Unendo i punti A,B,C,D,E si traccia il pentagono regolare.
Es.n4 Tav.5-Disegnare un esagono regolare inscritto nella circonf. di raggio r=50.
1)Tracciare la circonferenza di centro O e con raggio= 50.
2) Tracciare con segno misto fine gli assi principali, orizzontale e verticale, trovando sulla circonferenza i punti A e D.
3) Puntare in D con la stessa apertura di compasso precedente trovando sulla circonf. i punti E e C.
4) Ripetere l'operazione con centro nel punto A trovando i punti F e B sulla circonferenza.
5) Tracciare le linee evidenti e continue, con matita HB, che collegano i punti A, B, C, D, E e F, per ottenere l'esagono cercato.
Es n5- Tav. 7- Disegnare un ettagono inscritto nella circonferenza di raggio= 50
1.Tracciare la circonferenza di raggio r=50 e gli assi principali di simmetria trovando i 4 punti di intersezione fra circonferenza e gli Assi;
2.Puntare nel punto estremo destro di intersezione tra la circonf. e l'asse orizzontale. con apertura di compasso uguale al raggio della circonferenza , tracciare un arco e trovare i punti 1 e 2
3. Unire i punti 1 e 2 per trovare il punto M
4.Puntare in E con apertura 1-M, misura del lato dell'ettagono, tracciare un arco e trovare i punti D e F.
5.Riportare 5 volte la distanza 1-M sulla circonferenza, individuando i rimanenti punti dell'ettagono.
6.Unire i punti trovati ed evidenziare i lati dell’ettagono.
Es.n6 Tav.5-Regola generale per la suddivisione di una circonferenza in n parti uguali dato il raggio r=50
1. Tracciare la circonf.di raggio r=50.
2. Costruire i due assi principali, tra loro ortogonali, e prolungare quello orizzontale. Si individuano così i punti 0 (zero) e F.
3. Si applica il Teorema di Talete per dividere il segmento 0-F in 9 (numero di lati richiesto) parti uguali.
4. Puntare il compasso in F, con apertura uguale a F-0, e tracciare un arco che interseca l’asse orizzontale in Z e X.
5. Tracciare la semiretta che parte da Z e passa per il punto 7 della suddivisione dell’asse verticale. Procedere dalla parte opposta all'asse fino ad intersecare la circonferenza nel punto E.
6. Tracciare altre semirette che partono da Z e passano per 5, 3 e 1, ottenendo sulla circonferenza i punto D, C, e B.
7. Partendo dal punto X seguire la stessa procedura dei punti 5) e 6) per ottenere sulla parte opposta della circonferenza i punti G, H, I.
8. A,B,C,D,E,F,G,H,I sono i vertici dell’ennagono cercato. Unirli con segno continuo evidente.
 TECNOLOGIE E TECNICHE DI
RAPPRESENTAZIONE
GRAFICA CLASSI PRIME ISTITUTO TECNICO
SITO CURATO dalla Prof.ssa MARISTELLA MENIN
TECNOLOGIE E TECNICHE DI
RAPPRESENTAZIONE
GRAFICA CLASSI PRIME ISTITUTO TECNICO
SITO CURATO dalla Prof.ssa MARISTELLA MENIN

